Equazione della retta

Disegniamo su di un piano un sistema di assi cartesiani ortogonali di ascissa x ed ordinata y; tracciamo una retta r passante per l'origine degli assi il punto  O(0,0);

La retta tracciata è il grafico di una funzione di primo grado; vediamo ora di scrivere l'equazione di questa funzione.

Consideriamo i tre triangoli OAA', OBB', OCC' essi sono tre triangoli simili.

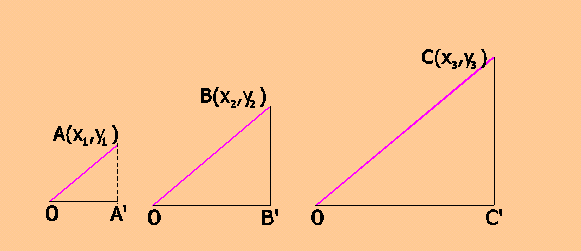tre triangoli simili

Sono simili in quanto hanno in comune l'angolo in O; essendo simili, oltre ad avere uguali anche gli altri due angoli, hanno pure i tre lati, corrispondenti ad ogni angolo, proporzionali. Scegliendo i lati paralleli ai due assi, otteniamo:

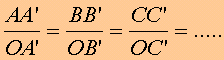
Ma, essendo:

AA'= y₁

BB'=y₂

CC'=y₃

.....

ed inoltre:

OA'=x₁

OB'=x₂

OC'=x₃

....

otteniamo:

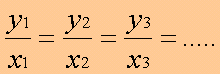
questo vuol dire che facendo il rapporto tra l'ordinata y e l'ascissa x otteniamo un numero costante, che possiamo indicare con la lettera m, e scrivere:

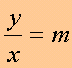
oppure:

 y=mx

Dove con x e y abbiamo indicato le coordinate di un generico punto P(x;y) scelto a piacere. Poiché i punti li abbiamo scelti a piacere sulla retta, possiamo affermare che l'equazione è valida per qualunque punto P(x;y) della retta r.

Possiamo, inoltre, definire la retta come l'insieme di punti che soddisfano l'equazione di primo grado:

y=mx

Il coefficiente m si chiama coefficiente angolare della retta r; m è detto anche pendenza della retta r. 

Dal valore di m dipende l'angolo a che la retta r forma con il verso positivo dell'asse x.

Se m>0 la retta forma, con il verso positivo dell'asse x, un angolo acuto, che va da 0° fino a 90°. Questo è dovuto al fatto che le due coordinate dei punti che appartengono alla retta sono di segno concorde, cioè o tutti e due positivi, e quindi appartengono al primo quadrante, oppure tutti e due negativi, e quindi appartengono al terzo quadrante.

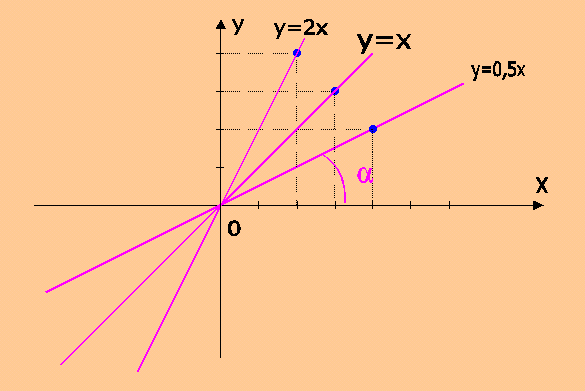se le due coordinate sono negative le rette appartengono al terzo quadrante

L'angolo che la retta forma, con il verso positivo dell'asse x, è acuto.

All'aumentare di m da 0 a ¥  l'angolo a aumenta da 0° fino a 90°. Vediamo ora due casi particolari di m, e cioè m=0 ed m=¥ .

1° caso : m=0

Quando m=0 l'angolo a =0°.

La retta r è, quindi, orizzontale e passa per l'origine degli assi O(0,0). 

Dalla equazione:

y=mx

essendo m=0 otteniamo:

y=0

La equazione y=0 rappresenta una retta parallela all'asse x e che passa per l'origine O(0,0), quindi rappresenta lo stesso asse x.

2° caso : m=¥

In particolare se m=¥  si ha che a=90°. Questo è un caso particolare di retta. Dalla equazione:

y=mx

ci ricaviamo la x, facendo la formula inversa, ed otteniamo:

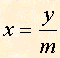
Ponendo m=¥ otteniamo

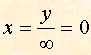
Nella frazione, essendo il denominatore un numero molto grande, precisamente ¥ , possiamo ritenere che il valore della frazione stessa sia molto piccolo, quindi nullo, e porre x=0. La equazione x=0 rappresenta una retta parallela all'asse y e che passa per l'origine O(0,0), quindi rappresenta lo stesso asse y.

Coordinate di segno discorde

Se le due coordinate x ed y sono di segno discorde, cioè l'una positiva e l'altra negativa, il valore di m sarà negativo, quindi:

m<0

Questo vuol dire che le rette si trovano o nel secondo quadrante, con x negative ed y positive, oppure nel quarto quadrante, con x positive e y negative.

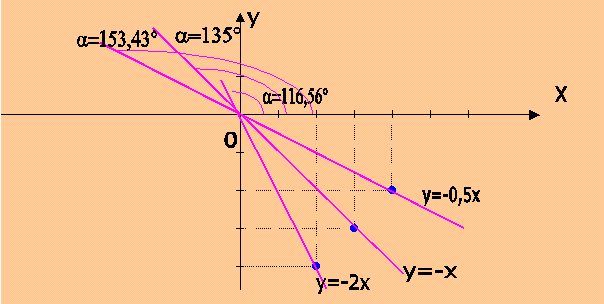
grafico di tre rette con m=-2; -1; -0,5

L'angolo che la retta forma con il verso positivo dell'asse x è ottuso.

Retta che non passa per l'origine degli assi

L'equazione:

y=mx

indica sempre una retta che passa per l'origine degli assi. Se aggiungiamo alla suddetta equazione una costante q,

y=mx + q

la retta si sposta verso l'alto, se q>0; si posta verso il basso se q<0. Ma resta sempre parallela alla retta di equazione:

y=mx

in quanto ha lo stesso coefficiente angolare m.

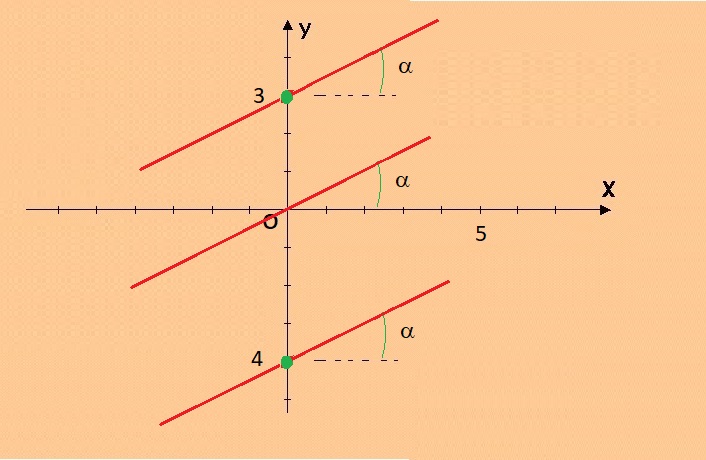grafico di tre rette con m=0,5 e a=26,56°

Il punto di intersezione con l'asse y si ottiene imponendo che x=0 nella equazione:

y=mx + q

Quindi:

y = q

La prima retta della figura di sopra ha equazione:

y = 0,5x + 3

La seconda retta della figura di sopra ha equazione:

y = 0,5x + 0

La terza retta della figura di sopra ha equazione:

y = 0,5x - 4

Quindi la costante q è l'ordinata che la retta ha nel punto dell'origine degli assi O(0;0)

Equazione implicita ed esplicita della retta

La equazione:

y=mx + q

è detta equazione esplicita della retta r.

Portando al primo membro e cambiando di segno, nella equazione esplicita:

y=mx + q

ottengo:

y - mx - q = 0

Questa equazione può essere scritta anche come:

ax + by + c = 0

cioè come un polinomio di primo grado nelle due variabili x ed y.

Essendo b diverso da zero, abbiamo messo: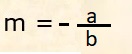

 

e

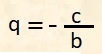
nella equazione:

y - mx - q = 0

Infatti, sostituendo, abbiamo:

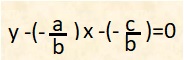
da cui, moltiplicando per b, ottengo:

by+ax+c=0 e quindi:

ax + by + c = 0

Questa equazione è detta equazione implicita della retta r.

L'equazione implicita della retta è sempre valida, anche quando la retta è parallela all'asse y ed ha, quindi, equazione:

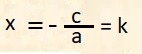
dove k è il punto di intersezione di r con l'asse x.

Essendo

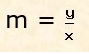
non possiamo calcolare m quando x=0, anche se m tende ad infinito per x=0.

Per queste rette non possiamo usare la forma esplicita:

y=mx + q

ma solo la forma implicita:

ax + by + c = 0

Vi sono dei casi particolari della retta r nella forma implicita.

ax + by + c = 0

 

Siano:

a=0   b≠0   c≠0

L'equazione diventa:

by + c = 0

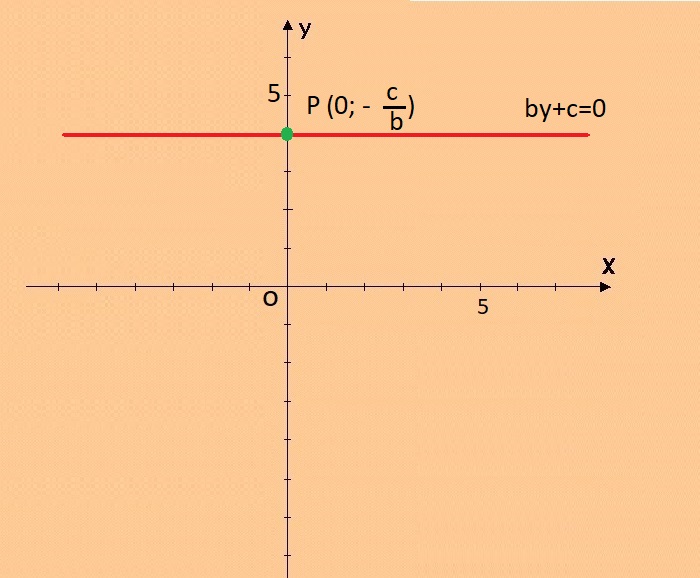grafico della retta by+c=0

La retta è parallela all'asse x e incontra l'asse y nel punto di coordinate:

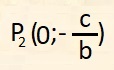
Ad essa appartengono tutti i punti aventi coordinate:

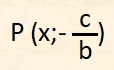
per qualunque valore di c; se c=0 si ha l'asse delle x.

Sia un altro caso particolare della retta di equazione:

ax + by + c = 0

cioè siano:

a≠0   b=0   c≠0

L'equazione diventa:

ax + c = 0

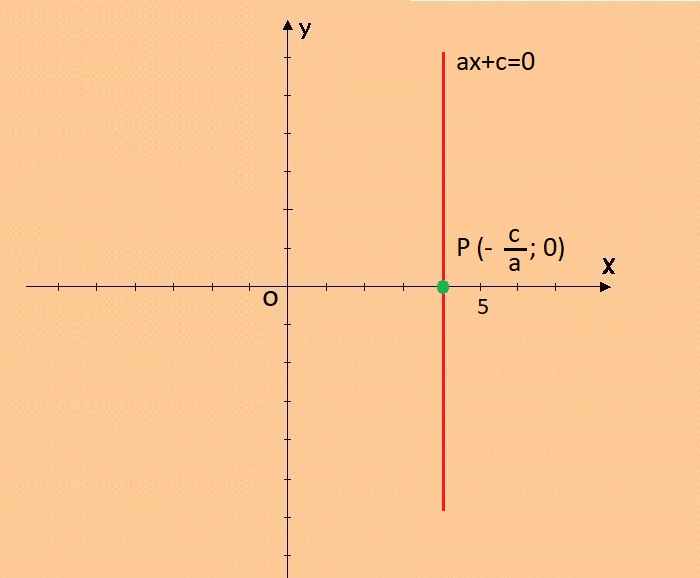grafico della retta ax+c=0

La retta è parallela all'asse y e incontra l'asse x nel punto di coordinate:

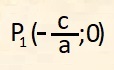
Ad essa appartengono tutti i punti aventi coordinate:

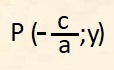
per qualunque valore di c; se c=0 si ha l'asse delle y.

Sia un altro caso particolare della retta di equazione:

ax + by + c = 0

cioè siano:

a≠0   b≠0   c=0

L'equazione diventa:

ax + by = 0

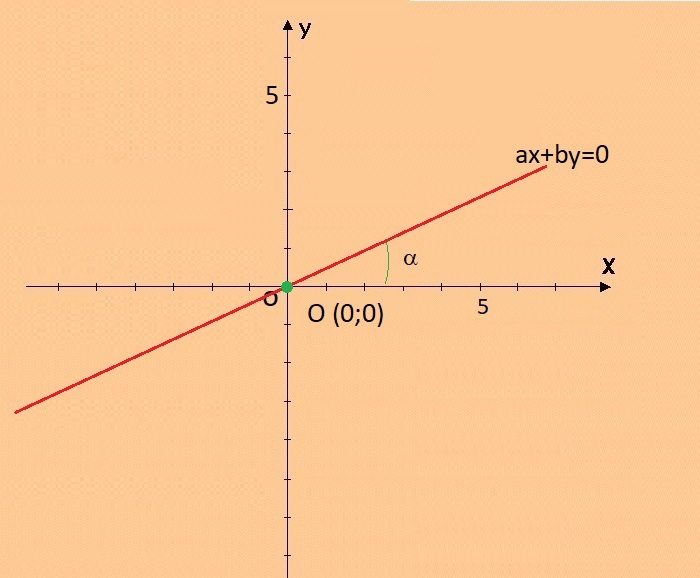
grafico della retta ax+by=0

La retta non è parallela a nessuno dei due assi, ma li incontra nell'origine degli assi; cioè la retta passa dal punto di coordinate:

Ad essa appartengono tutti i punti aventi coordinate:

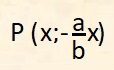
per qualunque valore di a e di b, ma con c=0.

Se, invece, anche c≠0 si ha il caso più generale, di una retta.

Cioè siano:

a≠0   b≠0   c≠0

L'equazione è:

ax + by + c = 0

 

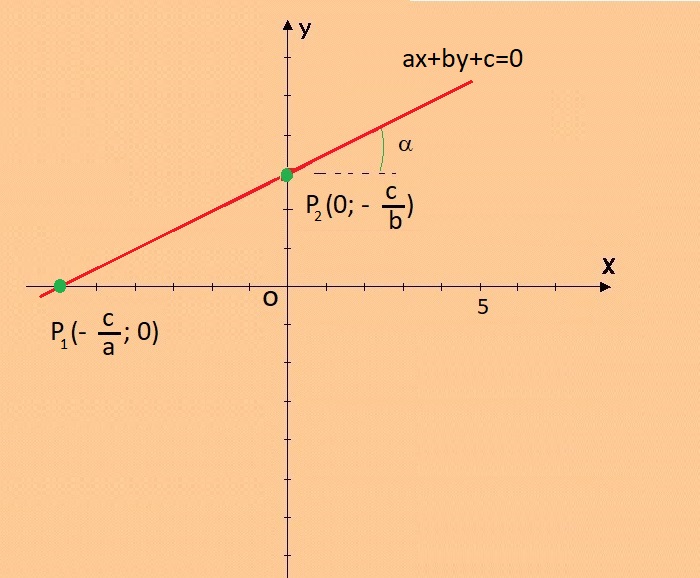
grafico della retta ax+by+c=0

La retta non è parallela a nessuno dei due assi.

La retta incontra l'asse y nel punto:

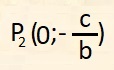
La retta incontra l'asse x nel punto:

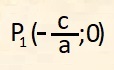
Ad essa appartengono tutti i punti aventi coordinate:

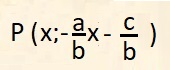
per qualunque valore di a, di b e di c, tutti diversi da zero.

Esempio

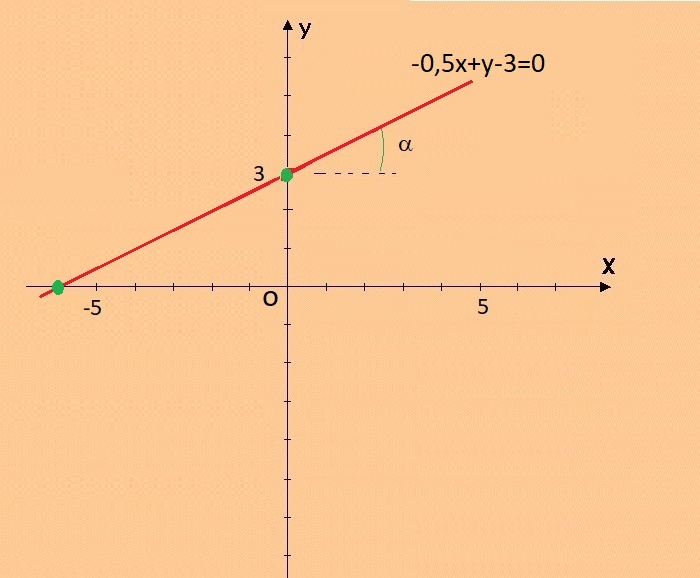
grafico della retta -0,5x+y-3=0

L'equazione sia:

-0,5x + y - 3 = 0

La retta incontra l'asse x nel punto:

P₁(-6;0)

La retta incontra l'asse y nel punto:

P₂(0;3)

Ad essa appartengono tutti i punti aventi coordinate:

P(x; 0,5x+3)

per qualunque valore di x.

 

Conclusione

Possiamo concludere che la equazione

ax + by + c = 0

detta equazione implicita della retta r, è sempre valida, per qualunque valore di a e di b, e per qualunque valore di x ed y.

Il caso a=0 e b=0 non ha significato, in quanto l'equazione:

ax + by + c = 0

diventerebbe:

c=0

e non avrebbe alcun significato geometrico corrispondente ad una retta nel piano cartesiano.

Esercizi

 

Lezioni di geometria analitica

 

Domanda al professore ( a pagamento )

Indice di tutto il sito